三角函数公式
三角函数公式是初高中必须掌握的,本文主要介绍所有的三角函数公式。
常用关系式
01、
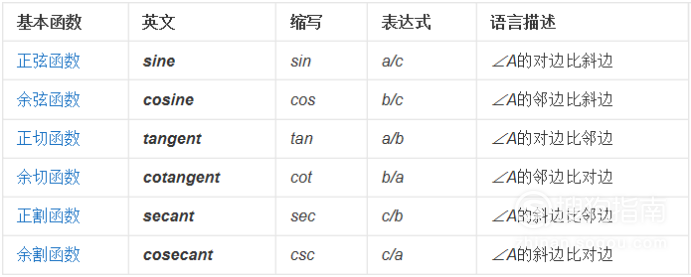
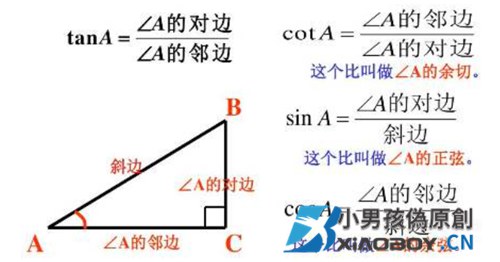
直角三角函数的定义:正弦(sin)等于对边比斜边;sinA=a/c ;余弦(cos)等于邻边比斜边;cosA=b/c ;正切(tan)等于对边比邻边;tanA=a/b ;余切(cot)等于邻边比对边;cotA=b/a;
 02、
02、
对角相乘乘积为1,即sinθ·cscθ=1; cosθ·secθ=1; tanθ·cotθ=1。
 03、
03、
商的关系:sinα/cosα=tanα=secα/cscα ;cosα/sinα=cotα=cscα/secα ;
 04、
04、
两角和差公式: tan(α+β)=(tanα+tanβ)/(1-tanαtanβ); tan(α-β)=(tanα-tanβ)/(1+tanαtanβ); cos(α+β)=cosαcosβ-sinαsinβ; cos(α-β)=cosαcosβ+sinαsinβ; sin(α+β)=sinαcosβ+cosαsinβ; sin(α-β)=sinαcosβ -cosαsinβ
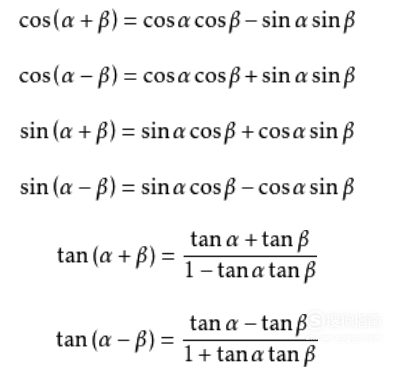 05、
05、
降幂公式sin²α=[1-cos(2α)]/2;cos²α=[1+cos(2α)]/2;tan²α=[1-cos(2α)]/[1+cos(2α)];
 06、
06、
二倍角公式:正弦:sin2α=2sinα·cosα ; 余弦:Cos2α=Cos^2(α)-Sin^2(α) ; Cos2α=1-2Sin^2(α) ; Cos2α=2Cos^2(α)-1 ;即Cos2α=Cos^2(α)-Sin^2(α)=2Cos^2(α)-1=1-2Sin^2(α);正切tan2α=(2tanα)/(1-tan^2(α));
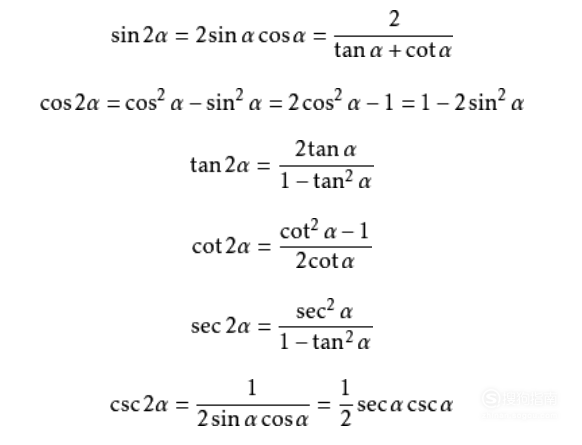 07、
07、
辅助角公式:asinx+bcosx=√(a²+b²)sin(x+φ)tanφ=b/a,φ的象限由a和b决定;
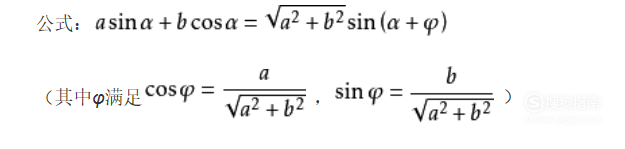 08、
08、
半角公式:
 09、
09、
常用特殊角:
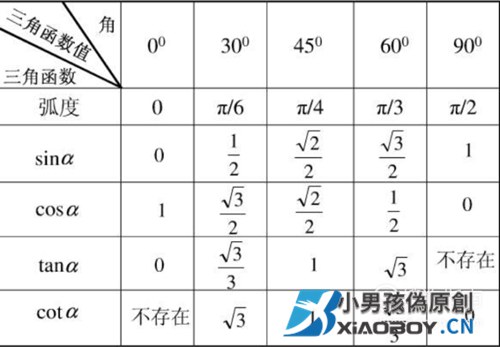 End 01 02 03 04 05
End 01 02 03 04 05
不常用的关系式
01、
万能公式:sinα=2tan(α/2)/[1+tan^2(α/2)] ;cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)] ;tanα=2tan(α/2)/[1-tan^2(α/2)];
 02、
02、
半角公式 tan(α/2)=(1-cosα)/sinα=sinα/(1+cosα); cot(α/2)=sinα/(1-cosα)=(1+cosα)/sinα; sin^2(α/2)=(1-cos(α))/2; cos^2(α/2)=(1+cos(α))/2; tan(α/2)=(1-cos(α))/sin(α)=sin(α)/(1+cos(α)) ;
 03、
03、
和差化积: sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]; sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]; cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]; cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]; tanθ+tanφ=sin(θ+φ)/cosθcosφ=tan(θ+φ)(1-tanθtanφ); tanθ-tanφ=sin(θ-φ)/cosθcosφ=tan(θ-φ)(1+tanθtanφ)
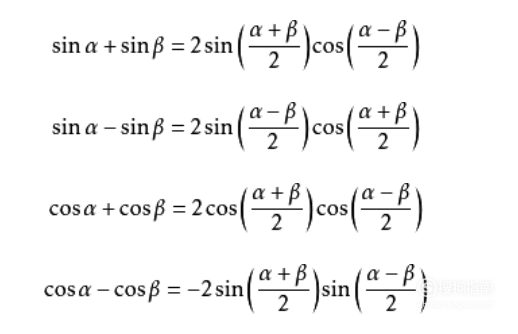 04、
04、
积化和差公式:sinαsinβ =-[cos(α+β)-cos(α-β)] /2;cosαcosβ = [cos(α+β)+cos(α-β)]/2;sinαcosβ = [sin(α+β)+sin(α-β)]/2;cosαsinβ = [sin(α+β)-sin(α-β)]/2;
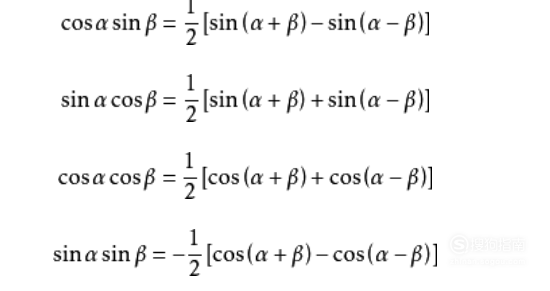 05、
05、
三角和:sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)÷(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)
 End
End
特别提示
此教程仅供参考,如有疵漏请谅解!